ORIGINAL ARTICLE
Machine learning based efficient routing protocol in wireless sensor network
Protocolo de enrutamiento eficiente basado en aprendizaje automático para redes de sensores inalámbricas
Shankar
Madkar1 ![]() *, Sanjay
Pardeshi2
*, Sanjay
Pardeshi2 ![]() *, Mahesh Shivaji Kumbhar3
*, Mahesh Shivaji Kumbhar3 ![]() *
*
1Shivaji University. Kolhapur, India.
2Government Residence women Polytechnic Tasgaon. Sangli, India
3Rajarambapu Institute of Technology, Department of E&TC. Rajaramnagar, India.
Cite as: Madkar S, Pardeshi S, Kumbhar MS. Machine learning based efficient routing protocol in wireless sensor network. Salud Cienc. Tecnol. 2022; 2(S2):195. https://doi.org/10.56294/saludcyt2022195
Submitted: 23-11-2022 Revised: 16-12-2022 Accepted: 24-12-2022 Published: 31-12-2022
ABSTRACT
Data loss and recovery are important factors that directly affect the efficiency of the wireless sensor network (WSN). The wireless channel characteristics have a significant impact on data transmission and reception. On the receiver side, the most difficult tasks are maximizing packet delivery ratio and recovering lost data. In some cases, cyclic redundancy check (CRC) based algorithms can provide better data recovery. The CRC method can be made adaptive by using channel characteristics to correct the error bits. This paper evaluates the performance of the proposed machine learning-based efficient routing protocol (ML-ERP). For data recovery, the CRC with channel impulse response (CIR) prediction based on sensor node location information was used. The data recovery capability of ML-ERP increased the network efficiency in terms of packet delivery ratio. Also, due to less data loss, the energy efficiency of the network was also improved by almost 6 % over existing protocols.
Keywords: ML-ERP; WSN; CRC; CIR; Data Recovery; Machine Learning.
RESUMEN
La pérdida y recuperación de datos son factores importantes que afectan directamente a la eficiencia de la red de sensores inalámbricos (WSN). Las características del canal inalámbrico tienen un impacto significativo en la transmisión y recepción de datos. En el lado del receptor, las tareas más difíciles son maximizar el ratio de entrega de paquetes y recuperar los datos perdidos. En algunos casos, los algoritmos basados en la comprobación de redundancia cíclica (CRC) pueden proporcionar una mejor recuperación de los datos. El método CRC puede hacerse adaptativo utilizando las características del canal para corregir los bits de error. Este trabajo evalúa el rendimiento del protocolo de enrutamiento eficiente basado en aprendizaje automático (ML-ERP) propuesto. Para la recuperación de datos, se utilizó el CRC con predicción de respuesta al impulso del canal (CIR) basada en la información de localización de los nodos sensores. La capacidad de recuperación de datos de ML-ERP aumentó la eficiencia de la red en términos de ratio de entrega de paquetes. Además, debido a la menor pérdida de datos, la eficiencia energética de la red también mejoró en casi un 6 % respecto a los protocolos existentes.
Palabras clave: ML-ERP; WSN; CRC; CIR; Recuperación de Datos, Machine Learning.
INTRODUCTION
Due to the wide range of applications that wireless sensor networks (WSNs) can have, there has been a lot of interest inthese networks recently. These are used to boost production efficiency in a variety of applications in industry.
In the field of ratings based recommendation systems, missing entry filling is performed to get ratings for unrated entries. This task is analogous to filling missing bits. Matrix factorization-based techniques for minimum error data recovery are popular in such data mining applications. It has recently been demonstrated that implementing the Matrix Completion (MC) technique, which is thought of as an extension of compressive sensing (CS), enhances wireless network efficiency. If the received data matrix has a low-rank structure, the partially received elements can be used to recover it with high accuracy.(1) Data is first directly detected in compressed form, and then the energy-intensive high-energy recovery process is carried out by the sink node. The computing complexity is thereby moved from the sensor nodes to the sink. This reduces energy consumption while simultaneously meeting the needs of devices with limited resources.
Thus the matrix completion method is useful for data recovery in signal processing applications, as the signal is composed of a time domain. The correlation coefficients that are required during data recovery are thus useful for the MC method. There is common data amongst sensors belonging to the same region, and such redundancy can be correlated in dense WSNs. In addition, the channel characteristics for each sensor node are different as per a change in location. The clustering algorithm can be applied for zonal segmentation of these sensor nodes. In such network configurations, cluster head (CH) based data aggregation becomes efficient and energy intensive, as all the CHs have common goals. This requires composition of a set of rules for all CHs in the network while collecting and forwarding the data. Using MC theory, the active nodes transmit their readings to the sink. However, some nodes are silent and do not take part in sensing. The twofold compression method is the updated version on paper.(2)
In contrast to Kortas et al.(2) cluster heads in WSN are chosen to have good links with the most nodes within the zone. During CH charging, nodes must gather various information from sensor nodes in addition to sensed data. This shows both control packet overhead along with data packet overhead may give rise to traffic. The increased traffic is the main cause of congestion events within the network.(3) MC theory can provide much more robust data recovery capability with the deterministic approach of selecting active nodes.(4,5)
The work presented in this paper is based on data recovery and efficient routing in WSN. The machine learning based efficient routing protocol (ML-ERP), which can be used in WSN, is presented. The cyclic redundancy check (CRC) with use of channel impulse response (CIR) method was developed. The machine learning based approach was used for predicting the channel characteristics, which reduces the computational complexity, thereby improving the efficiency in terms of packet delivery ratio, energy consumption, and average end to end delay.
Literature survey
This section discusses data recovery techniques used in wireless networks and wireless sensor networks. The significance of CS theory is addressed by referring to techniques from several researchers in the field.
The coefficient based representation of data is feasible as WSN signal patterns are dependent in both the time and space domains. The sparse nature of the data is responsible for increasing the complexity in data recovery mechanisms. Also, it has been shown(6,7) that a low dimensional architecture for recovering possibilities is an important aspect. Signal capture and reconstruction using coefficients is thus possible in such applications.
Kumar et al.(8) show the suitability of CS for such a recovery. Data recovery from signals is more precise with CS theory as the degree of sparsity increases. Most of the cases can be observed with a Nyquist criteria based approach where information signal characteristics play an essential role.(9,10,11) Under-determined linear systems have been addressed using efficient convex relaxation and greedy pursuit-based techniques like NESTA.(12) In a similar war way L1-MAGIC(13) also works. The sparsity is addressed with the use of orthogonal matching pursuit (OMP).(14)
Along with lowering the recovery error, the channel characteristics were used to recover the incoming data matrix's empty columns. There was a chance that there could be empty columns because the measurements were sent based on a presence probability. On the other hand, Zhou et al.(15) used an MC technique based on Bayesian inference and the temporal stability feature to interpolate missing data.
Fragkiadakis et al.(16) also contemplated combining MC with CS. Prior to employing the MC to recover any lost or unsampled data, they employed the CS to compress the sensor node readings. However, it has not been compared to other cutting-edge ways to demonstrate this approach's true value. The signal space time correlation becomes crucial during the CS based approach which mainly focuses on compression and sparseness of the signals.
The approach proposed by Wang and cols., (17) is overcome for sparsity problems by He et al.(18) in which the graph-based transform sparsity approach is used. K. Xie et al.(19,20) shown the constrained optimization problem was resolved in the decoding part by integrating the sparsity and low-rank features and employing multipliers in the alternating direction.
Machine learning has shown dominance in every field today. During data recovery in WSNs, machine learning approaches are also considered and it has been discussed the uses of machine learning in WSN applications.(21) The unsupervised learning along with use of k mean clustering and principal component analysis (PCA) are discussed along with multiple challenges while applying machine learning in WSN. Use of redundant data due to common data generation from multiple nodes within the same zone is used for internet of things (IoT) applications. The machine learning based multiple attributes method is used to predict the lost data and fill the missing data. The efficiency improvement is shown with the use of machine learning methods.(22)
Moreover, a deep learning strategy with the use of convolutional neural network (CNN) for data recovery in health monitoring WSN.(23) The structured data communication pattern is considered in this method. The missing data from the structure is predicted using CNN model where predefined structured data is used for training purposes. The unsupervised machine learning strategy is evaluated for information centric WSNs.(24)
The problem with MC recovery in the presence of subsequent data loss or corruption, known as structure defects, is that data loss due to fading characteristics of the channel or sensor node failure leads to missing data.(6)
Based on multiple studies, the channel characteristics and MC theory can be correlated to efficiently recover the data along with machine learning methods. Our work considers channel characteristics as a critical parameter that can meet the requirement for assessing data recovery. Regression-based data prediction is employed for channel characteristics prediction, and CRC based recovery was used for recovering the messages that are communicated with an encoding-decoding-based approach.
Proposed work
The main objective of the proposed work was to recover lost data in WSN. Data recovery is now handled more efficiently in networks based on 3G or LTE. During the recovery process, the data received is encrypted. This shows the problem of easy guessing for rounding off techniques during the recovery process. The Linear Feedback Shift Register is used in today’s networks in which g(x) acts as a connection polynomial and the Cyclic Redundancy Check (CRC). The drawback of typical CRCs for detecting random errors is that they lack a reliable method for identifying bad information. By merging quick generator polynomial computing techniques with cryptographic hash functions, error-free communication in WSNs can be achieved. The proposed system for data recovery in WSN consists of the stages shown in figure 1.
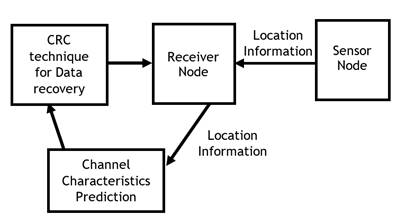
Figure 1. Proposed System Block diagram
Data recovery and Channel characteristics
The data recovery problem is similar to the missing entry filling. Popular algorithms, such as Matrix Completion(25), have shown significant improvement in data recovery.
The received data is calculated using impulse response equation as,
![]() ...
(1)
...
(1)
Hence,
![]()
where x(n) is the input data vector and h is the CIR matrix to get output data vector y(n). In equation (1) h can be calculated to get x(n) from received y(n) using node location information. Each calculation step of h may lead to a complex computational requirement when new location information from another node is received. To minimize the computational complexity, a neural network model can be used to predict the value of h. Predicted h is used for original data recovery in this work.
The CIR matrix h contains numeric data and hence, it is the regression work. The h' matrix can be predicted using a historical set of h'i matrices. During the training and testing phase, the proper estimation of h' for a new site is performed (xi, yi). The third value of noise, which varies based on the distance from a particular point, is an important component for extracting channel characteristics. As a result, the noise level is likely to be random, and the noise amplitude could vary in line with the characteristics of the Rayleigh channel.
The location data is used as the goal h value input vector while training a neural network. The machine learning experiment employed 100 data vectors of this type.
From the perspective of a generic application, the prediction of numerical data is a regression problem. First, the results of the matching item number prediction are verified using a linear regression model. The growing mean square error is seen in the data. The multiple regression model is employed because of the substantial amount of input data vectors. Multiple collinearity and errors from non-normal data are significant factors in multiple regression analysis. The coefficients exhibit non-correlated features when ordinary least square estimations are performed on the explanatory variables. A linear regression formula,
![]() (2)
(2)
where the goal vector is Y and the input vector is X.
The least square estimates for parameter are provided by,
![]() (3)
(3)
The estimation of the value given by, using the minimization function
![]() (4)
(4)
Unbiased least squares (LS) in a normal distribution is the unbiased linear estimator with the lowest variance. On the other hand, it is impossible to interpret individual coefficients if the explanatory factors are highly correlated. Additionally, this method increases standard errors because of the coefficients' multicollinearity. Therefore, selecting the appropriate regression model is crucial.
Consequently, the best option to this least square is ridge regression. We prefer ridge regression over LS because it enhances the estimation with the addition of a diagonal constant to the matrix while having no bias but a high variance. Variance is decreased as a result of this technique. Ridge regression estimates this as,
![]() (5)
(5)
I is the PXP identity matrix in equation (3), and K is the unidentified biasing constant. K's value can be calculated as,
![]() (6)
(6)
where,
![]() (7)
(7)
To lower the mean square error and hence reduce variance, the bias value in ridge regression is increased. When the dataset is small, biasing parameters provide more effective variance control. With a large dataset and Bayesian regression, the performance minimizes variance and can be further improved. Using a large dataset and a probabilistic approach with Bayesian regression can raise the effective likelihood in the results of multiple regression. The formula for The Bayes' Theorem is,
![]() (8)
(8)
In Bayes' Theorem, probabilistic occurrences are taken into account together with events A and B, and P stands for the corresponding probabilities.
There is a proportional relation in the posterior distribution of Ordinary Least Square (OLS) and likelihood, as in the preceding calculation.
A huge dataset could be used to boost this likelihood. The increased likelihood of forecasting with the least amount of mean square error (MSE) is the parameter of evaluation. The Bayesian ridge regression mathematical model is provided by,
![]() (9)
(9)
where λ is the proportion of bias to variance in squared terms for weights w at input I at point p. Bayesian Regression based efficient routing protocol ML-ERP is developed. The algorithm for ML-ERP is explained here. Algorithm:
1. Initialize the network.
2. Collect location information from all sensor nodes.
3. Calculate CIR matrices for each location using machine learning method.
4. Start receiving the data from transmitting nodes.
5. Apply CRC for recovering lost bits with use of CIR.
RESULTS AND ANALYSIS
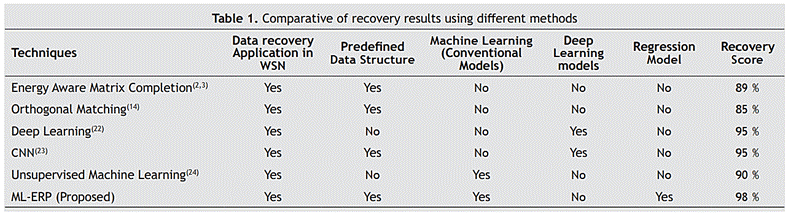
A comparison of different methods based on the use of different attributes is shown in Table 1.
The network configuration parameters are detailed in Table 2. When analyzing the performance of the data recovery model proposed in this work, the network configuration was critical. The amount of data sent, lost during communication, and recovered by using the recovery method was the main strategy followed in the experimental study. Figure 2 shows the network deployed during experimentation.

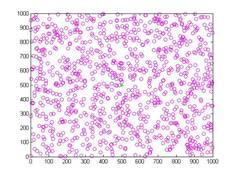
Figure 2. Sensor nodes deployed with Sink node at the centre
Dataset Prep
The training of regression models was performed. Figure 3 and 4 show MSE and RMSE analysis on the predictions. Equation (10) and (11) show MSE and RMSE analysis.
![]() (10)
(10)
![]() (11)
(11)
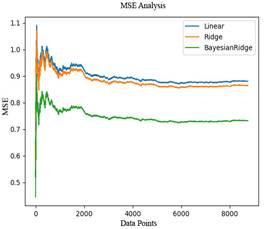
Figure 3. Regression model prediction MSE analysis
Based on MSE and RMSE analyses, the Bayesian Regression Model was found to be better. This model was compared with other models.
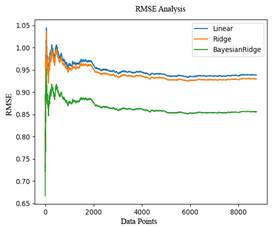
Figure 4. Regression model prediction RMSE analysis
Manel Kortas et al.(25) have given a technique that is based on the Matrix Completion (MC) methodology with the use of matrix factorization. Decomposition and multiple iterations of multiplication are performed in matrix factorization for missing data recovery by comparing known values with the multiplication outcome. The calculations are either continued in terms of error threshold or stopped after a certain number of iterations. This method shows the dependency on the number of missing values and their closest match requirement when matrix factorization is applied. The closest match may thus require a large number of iterations, which may consume a significant amount of computational time and increase network latency.
Inter-node correlation is considered to present a complementary minimization problem. Interpolation increases the likelihood of recovering readings lost due to channel effects or node failures.
The comparative best performing Bayesian Regression from the proposed work is compared with MC.(25) The results of comparison are shown in figure 5. Bayesian regression showed an improvement in performance over MC(25) in terms of RMSE, MSE.
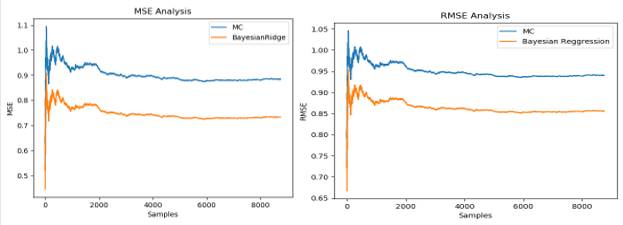
Figure 5. Comparison of MC and proposed method for MSE and RMSE analysis
Figure 6 shows the amount of data lost during communication in a 100 nodes scenario and the amount of data recovered compared to the total amount of data sent by using MC(25) and Bayesian Regression based methods.
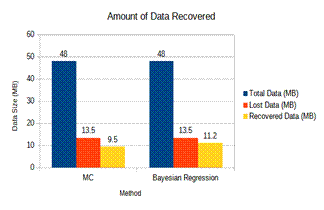
Figure 6. Comparative analysis of amount of data recovered
In WSN, models are deployed to analyze the packet delivery ratio and energy efficiency. The residual energy analysis was performed by comparing the performance with other WSN protocols. To evaluate the performance of ML-ERP, it was compared with the LEACH,(26) HM2LP,(27) EESAA,(28) EESRA,(29) M-IWOCA(30) protocols.
The Low Energy Adaptive Clustering Hierarchy (LEACH)(26) protocol simply uses the clustering in the network to improve the routing efficiency. The sleep mode is enabled during idle state of the sensor nodes and cluster head (CH) in Energy Efficient Sleep Awake Aware (EESAA)(28) protocol. The CG node aggregated the cluster's data, which was then passed on to the CH via the energy-efficient scalable routing algorithm (EESRA).(29) Modified-Invasive Weed Optimization Based Clustering Algorithm (M-IWOCA)(30) uses a specific CH selection strategy such that it improves the network lifetime of the network compared to LEACH.
The lifetime analysis was performed for energy efficiency estimation of all the protocols. The first node died and the last node died in the total rounds of communication in the network analyzed. Figure 7 shows the lifetime analysis.
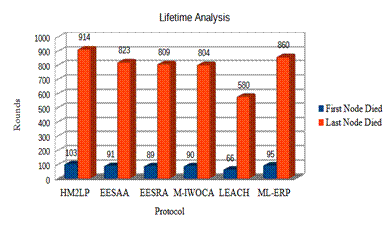
Figure 7. Comparative of Lifetime Analysis
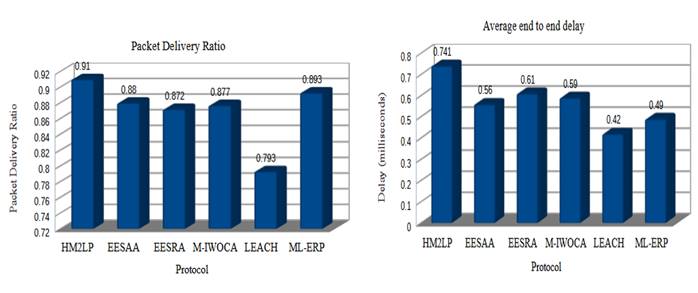
Figure 8. Packet delivery ratio and average end to end delay
Figure 8 shows the comparative analysis performed for packet delivery ratio and average end to end delay. The proposed ML-ERP shows 49 milliseconds of average end to end delay for the data of ten thousand packets. As LEACH has less computational complexity compared to other protocols, it has a very low average end to end delay. The packet delivery ratio of the HM2LP (27) protocol is better due to the virtual base stations formed with the use of rendezvous nodes. Hence, communication distance is less, which improves the chances of better reception. On the other hand, even with long distance communication in the proposed ML-ERP protocol, the packet delivery ratio was almost 90 %.
CONCLUSION
This paper contributes to machine learning-based channel prediction and cyclic redundancy check-based data recovery in wireless sensor networks (WSN). The regression problem for channel impulse response matrix prediction with the use of Bayesian regression shows fewer errors and hence better data recovery capability.
The comparative analysis is done with matrix factorization based data recovery, and it is found that the matrix factorization is dominated in terms of RMSE and MSE by the proposed method. Almost 98 % data is recovered during experimental analysis.
The average end to end delay of 49 milliseconds and packet delivery ratio of 90% show satisfactory performance compared to other protocols during experimentation with the proposed machine learning based efficient routing protocol (ML-ERP).
The lifetime analysis shows an increase in the number of rounds compared to other protocols for network survival for up to complete energy run out of the network's last node. Further, if the addition of clustering and rendezvous nodes is done, thus there are chances to improve the performance of ML-ERP.
REFERENCES
1. Candès EJ, Recht B. Exact matrix completion via convex optimization. Found Comput Math. 2009;9:717. https://doi.org/10.1007/s10208-009-9045-5
2. Kortas M, Habachi O, Bouallegue A, Meghdadi V, Ezzedine T, Cances J. Energy efficient data gathering schema for wireless sensor network: a matrix completion based approach. In: Proceedings of the International Conference on Software, Telecommunications and Computer Networks. 2019. pp. 1-6. doi: 10.23919/SOFTCOM.2019.8903635.
3. Hung C, Peng W, Lee W. Energy-aware set-covering approaches for approximate data collection in wireless sensor networks. IEEE Trans Knowl Data Eng. 2012 Nov;24(11):1993-2007. doi: 10.1109/TKDE.2011.224.
4. Kortas M, Habachi O, Bouallegue A, Meghdadi V, Ezzedine T, Cances JP. The energy-aware matrix completion-based data gathering scheme for wireless sensor networks. IEEE Access. 2020;8:30772-30788. doi: 10.1109/ACCESS.2020.2972970.
5. Du R, Chen C, Yang B, Lu N, Guan X, Shen X. Effective urban traffic monitoring by vehicular sensor networks. IEEE Trans Veh Technol. 2015 Jan;64(1):273-286. doi: 10.1109/TVT.2014.2321010.
6. Xie K, et al. Recover corrupted data in sensor networks: a matrix completion solution. IEEE Trans Mob Comput. 2017 May 1;16(5):1434-1448. doi: 10.1109/TMC.2016.2595569.
7. Chen Y, Chi Y. Harnessing structures in big data via guaranteed low-rank matrix estimation. arXiv. 2018. https://doi.org/10.48550/arXiv.1802.08397
8. Kumar GE, Baskaran K, Blessing RE, Lydia M. A comprehensive review on the impact of compressed sensing in wireless sensor networks. Int J Smart Sens Intell Syst. 2016. doi: 10.21307/ijssis-2017-897.
9. Donoho DL. Compressed sensing. IEEE Trans Inf Theory. 2006 Apr;52(4):1289-1306. doi: 10.1109/TIT.2006.871582.
10. andes EJ, Wakin MB. An introduction to compressive sampling. IEEE Signal Process Mag. 2008 Mar;25(2):21-30. doi: 10.1109/MSP.2007.914731.
11. Eldar YC, Kutyniok G. Compressed Sensing: Theory and Applications. Cambridge University Press; 2012. DOI: 10.1017/CBO9780511794308.
12. Becker S, Bobin J, Candès EJ. NESTA: A fast and accurate first-order method for sparse recovery. SIAM J Imaging Sci. 2011;4:1-39. DOI: 10.1137/090756855.
13. Candes E, Romberg J. l1-magic: Recovery of Sparse Signals via Convex Programming. 2005. Volume 4, p.14. Available from: https://inst.eecs.berkeley.edu/~ee225b/sp08/lectures/CSmeetsML-Lecture1/codes/l1magic/l1magic.pdf
14. Cai TT, Wang L. Orthogonal Matching Pursuit for Sparse Signal Recovery with Noise. IEEE Transactions on Information Theory. 2011;57(7):4680-4688. DOI: 10.1109/TIT.2011.2146090.
15. Zhou H, Zhang D, Xie K. Accurate traffic matrix completion based on multi-Gaussian models. Comput Commun. 2017;102:165-176.
16. Fragkiadakis A, Askoxylakis I, Tragos E. Joint compressed-sensing and matrix-completion for efficient data collection in WSNs. In: Proceedings of the 2013 IEEE 18th International Workshop on Computer Aided Modeling and Design of Communication Links and Networks (CAMAD); 2013 Sep 25-27; Berlin, Germany. p. 84-88. DOI: 10.1109/CAMAD.2013.6708094.
17. Wang D, Wan J, Nie Z, Zhang Q, Fei Z. Efficient Data Gathering Methods in Wireless Sensor Networks Using GBTR Matrix Completion. Sensors. 2016;16:1532. DOI: 10.3390/s16091532.
18. He J, Sun G, Li Z, Zhang Y. Compressive data gathering with low-rank constraints for wireless sensor networks. Signal Process. 2017;131:73-76. DOI: 10.1016/j.sigpro.2016.08.002.
19. Xie K, Li X, Wang X, Xie G, Wen J, Zhang D. Active sparse mobile crowd sensing based on matrix completion. In: Proceedings of the 2019 International Conference on Management of Data; 2019 Jun 30-Jul 5; Amsterdam, Netherlands. p. 195-210. DOI: 10.1145/3299869.3319856.
20. Xie K, Wang L, Wang X, Xie G, Wen J. Low Cost and High Accuracy Data Gathering in WSNs with Matrix Completion. IEEE Transactions on Mobile Computing. 2018;17(7):1595-1608. DOI: 10.1109/TMC.2017.2775230.
21. Nath MP, Mohanty SN, Priyadarshini SB. Application of machine learning in wireless sensor network. In: Proceedings of the 8th International Conference on Computing for Sustainable Global Development (INDIACom); 2021. p. 7-12.
22. Cheng H, Shi Y, Wu L, Guo Y, Xiong N. An intelligent scheme for big data recovery in Internet of Things based on Multi-Attribute assistance and Extremely randomized trees. Information Sciences. 2021;557:66-83. doi: 10.1016/j.ins.2020.12.041.
23. Oh BK, Glisic B, Kim Y, Park HS. Convolutional neural network-based data recovery method for structural health monitoring. Structural Health Monitoring. 2020;19(6):1821-1838. doi: 10.1177/1475921719897571.
24. Pellenz ME, Lachowski R, Jamhour E, Brante G, Moritz GL, Souza RD. In-network data aggregation for information-centric WSNs using unsupervised machine learning techniques. In: Proceedings of the IEEE Symposium on Computers and Communications (ISCC); 2021. p. 1-7. doi: 10.1109/ISCC53001.2021.9631416.
25. Kortas M, Habachi O, Bouallegue A, Meghdadi V, Ezzedine T, Cances JP. Robust data recovery in wireless sensor network: a learning-based matrix completion framework. Sensors (Basel). 2021 Feb 2;21(3):1016. doi: 10.3390/s21031016. PMID: 33540836; PMCID: PMC7867355.
26. Heinzelman WR, Chandrakasan A, Balakrishnan H. Energy-efficient communication protocol for wireless microsensor networks. In: Proceedings of the 33rd IEEE International Conference on System Sciences. 2000. p. 1-10.
27. Rajput M, Sharma SK, Khatri P. HM2LP: Hybrid Multilevel Multihop LEACH Protocol for Conserving Energy in Large Area WSN. Int J Intell Eng Syst. 2022;15(2). doi: 10.22266/ijies2022.0430.03.
28. Ennaciri A, Erritali M, Bengourram J. Load balancing protocol (EESAA) to improve quality of service in wireless sensor network. Procedia Computer Science. 2019;151:1140-1145.
29. Elsmany EF, Omar MA, Wan T, Altahir AA. EESRA: Energy efficient scalable routing algorithm for wireless sensor networks. IEEE Access. 2019;7:96974-96983.
30. Sharma R, Vashisht V, Singh U. Fuzzy modeling based energy aware clustering in wireless sensor networks using modified invasive weed optimization. J King Saud Univ Comput Inf Sci. 2019.
CONFLICT OF INTEREST
The authors declared that there are no competing or conflicting interests.
FUNDING
None.
AUTHORSHIP CONTRIBUTION
Conceptualization: Shankar Madkar, Sanjay Pardeshi, Mahesh Shivaji Kumbhar.
Methodology: Shankar Madkar, Sanjay Pardeshi, Mahesh Shivaji Kumbhar.
Writing - Original Draft: Shankar Madkar, Sanjay Pardeshi, Mahesh Shivaji Kumbhar.
Writing - Review & Editing: Shankar Madkar, Sanjay Pardeshi, Mahesh Shivaji Kumbhar.